神经网络之多维卷积的那些事(一维、二维、三维)

前言

一般来说，一维卷积用于文本数据，二维卷积用于图像数据，对宽度和高度都进行卷积，三维卷积用于视频及3D图像处理领域（检测动作及人物行为），对立方体的三个面进行卷积。二维卷积的用处范围最广，在计算机视觉中广泛应用。

一维卷积Conv1d

一维卷积最简单，实质是对一个词向量做卷积，如下所示：

图中的输入的数据维度为8，过滤器的维度为5。卷积后输出的数据维度为8−5+1=4
如果过滤器数量仍为1，输入数据的channel数量变为16，则输入数据维度为8×16
一维卷积常用于序列模型，自然语言处理领域。

Pytorch中nn.Conv1d卷积运算要求输入源是3维，输入源的三个维度分别是：第一个维度代表每个序列的个数即样本数，第二个维度代表每一个序列的通道数，第三个维度代表这个词向量序列，如下所示：

import torch
import torch.nn as nn
# 输入源：1个样本，16个通道，8个数据
a = torch.randn(1,16,8)
# 卷积：输入通道为16，输出通道为1，卷积核大小 5*5
conv = nn.Conv1d(16, 1, 5)
c = conv(a)
print('a:', a.size())
print('c:', c.size())

output

1 2	a: torch.Size([1, 16, 8]) c: torch.Size([1, 1, 4])

二维卷积Conv2d

二维卷积是最常见、用途最广泛的卷积。先假定卷积核(过滤器)数量为1，图片通道数为1，卷积操作如下：

图中的输入的数据维度为14×14，卷积核数量为1，图片通道数为1
二维卷积输出的数据尺寸为8−5+1=4，即4×4

这是最简单的二维卷积的场景，现在重点来了，假定图片通道数为3，卷积核的数量为1，则卷积操作如下：

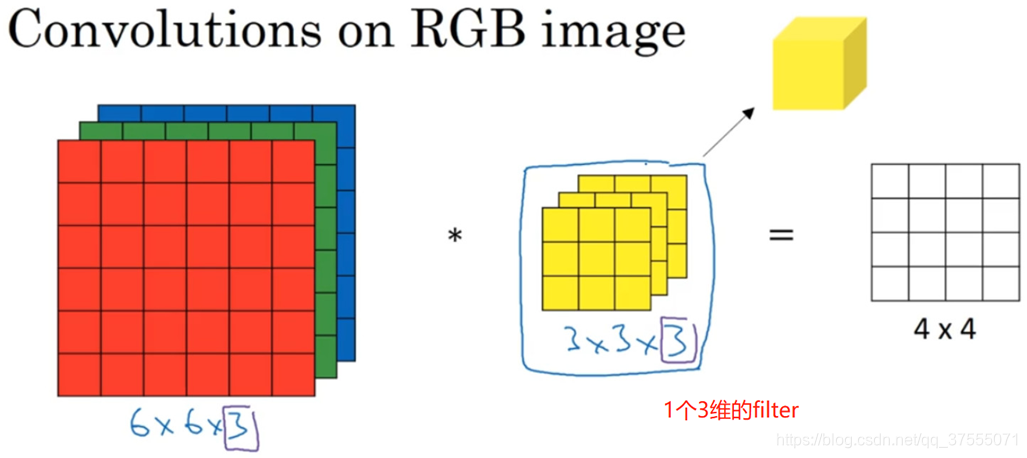
如上图所示，输入源是6*6*3（图片大小6*6,三个通道），卷积核大小3*3，filters(卷积核数量)=1,即权重矩阵是3*3*3*1，得到的结果4*4*1（图片大小4*4,一个通道）
其实就是三个3*3的卷积核分别对图片的三个通道做卷积，然后把结果相加得到一个4*4的图片。所以，这里卷积核w的参数个数是(3*3*3+1)*1，(输入通道3，卷积核大小3*3，一个偏置，输出通道1)
上图卷积 Pytorch中表示为：nn.Conv2d(3,1,kernel_size=(3,3),stride=1)

到这里可能有人会问，卷积核大小为3*3，为什么变成3*3*3了？
可以细想一下，图片的大小是6*6*3（图片大小6*6,三个通道），也就是三维的图片，二维的卷积是肯定不能对其操作的，所以卷积核的维度会随着图片的输入通道改变，如果图片的输入通道是3，那么卷积核的维度也是3，如果图片的输入通道是1，那么卷积核的维度也是1，这也就是为什么Pytorch中nn.Conv2d的输入通道要与图片的输入通道保持一致的原因，否则无法进行卷积操作。

现在，假定图片通道数为3，卷积核的数量为2，则卷积操作如下：

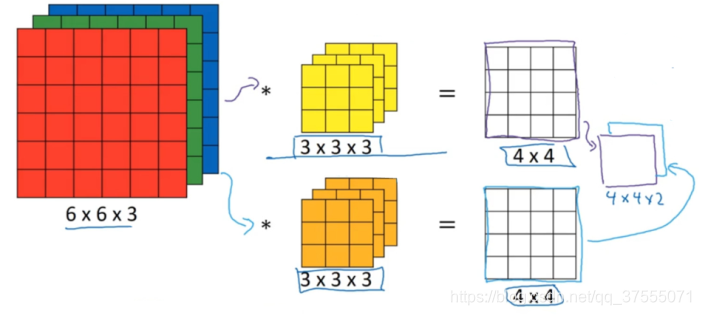
如上图所示，输入源是6*6*3（图片大小6*6,三个通道），卷积核大小3*3，filters=2，即权重矩阵是3*3*3*2，得到的结果4*4*2
上图每一个卷积核卷积参数的个数是(3*3*3+1)*2
上图卷积 Pytorch中表示为：nn.Conv2d(3,2,kernel_size=(3,3),stride=2)

计算图如下所示：

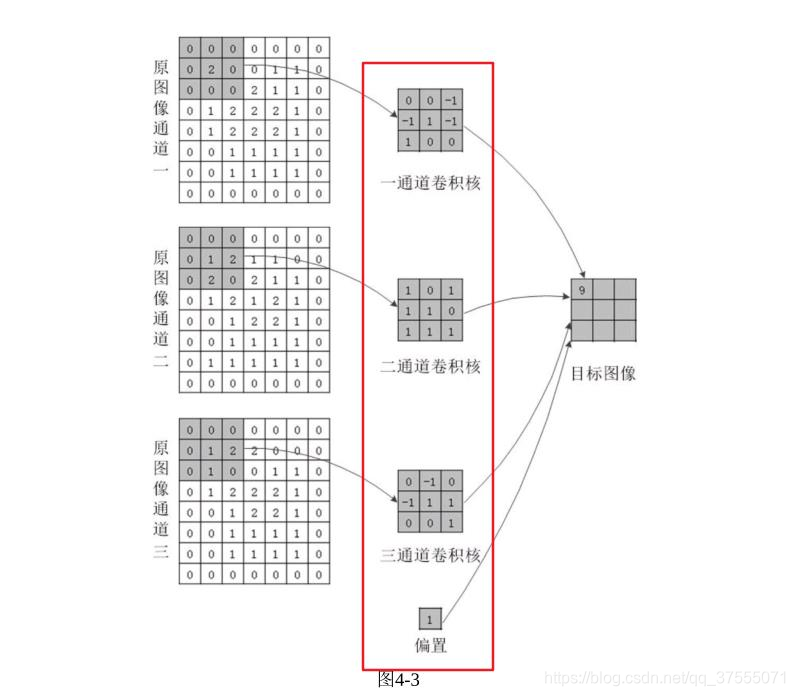
二维卷积常用于计算机视觉、图像处理领域。

Pytorch中nn.Conv2d卷积运算要求输入源是4维，输入源的四个维度分别是：第一个维度代表图片的个数即样本数，第二个维度代表每一张图片的通道数，后面二个维度代表图片的像素矩阵，如下所示：

import torch
import torch.nn as nn
a = torch.Tensor([[[[1,2,3,4],
                [5,6,7,8],
                [9,10,11,12],
                [13,14,15,16]]],
               [[[1,2,3,4],
                [5,6,7,8],
                [9,10,11,12],
                [13,14,15,16]]]])
print('a:',a.size())
# 卷积核：输入通道为1，输出通道6，卷积核大小2*2
conv = nn.Conv2d(1,6,2)
c = conv(a)
print('c:',c.size())

conv1 = nn.Conv2d(6,16,2)
c1 = conv1(c)
print('c1:',c1.size())

output

1
2
3

a: torch.Size([2, 1, 4, 4])
c: torch.Size([2, 6, 3, 3])
c1: torch.Size([2, 16, 2, 2])

三维卷积Conv3d

三维卷积具体思想与一维卷积、二维卷积相同，假设卷积核大小为f1*f2*f3(类似于二维卷积，三维卷积实际计算的时候卷积核是四维的，另一个维度由输入源的通道数决定)

假设输入数据的大小为a1×a2×a3
基于上述情况，三维卷积最终的输出为(a1−f1+1)×(a2−f2+1)×(a3−f3+1)
三维卷积常用于医学领域（CT影响），视频处理领域（检测动作及人物行为）。

Pytorch中nn.Conv3d要求输入源是5维的，输入源的5个维度分别表示为：第一个维度代表样本的个数，第二个维度代表每个样本的通道数，后面三个维度代表三维立体图形的像素矩阵，如下所示：

import torch
import torch.nn as nn
x = torch.randn(1,2,6,1,1)
conv = nn.Conv3d(in_channels=2,
                 out_channels=6,
                 kernel_size=(2,1,1))
c = conv(x)
print('x:', x.size())
print('c:', c.size())

output

1 2	x: torch.Size([1, 2, 6, 1, 1]) c: torch.Size([1, 6, 5, 1, 1])

说明：通道数从输入的2转化为6，一个立体像素矩阵，输入前大小为6*1*1, 卷积核2*1*1，得到结果为(6-2+1)*(1-1+1)*(1-1+1)=5*1*1

卷积中的特征图大小计算方式

在神经网络卷积操作主要是提取特征的，因此卷积的输出称为特征图(FeatureMap)，神经网络中有多层卷积，所以除了最开始输入的原始图像外，我们认为卷积输入的也是特征图

当卷积操作步长为1的时候，进行卷积操作后特征图的尺寸比较容易计算，如果步长为2或者更大就不容易计算了。其实这里有一个通用的公式，如下所示：

W_{out} = \frac{ W_{in}+2*padding-K}{stride} + 1

其中， $W_{out}$ 为输出特征图的大小， $W_{in}$ 为输入特征图的大小，K为卷积核大小，stride为卷积步长，padding为特征图填充的圈数。

这里不得不提一下，池化操作对上述公式也适用，我看有的文章里说，卷积除不尽的结果都向下取整，池化除不尽的结果都向上取整，这个说法是错误，我经过测试得出Pytorch和TensorFlow默认都是向下取整。如下所示：

卷积操作向下取整

# 卷积操作向下取整
import torch
import torch.nn as nn
a = torch.rand(1,1,10,10)
# (10+2*2-5)/2.0+1 = 5.5
conv2d = nn.Conv2d(in_channels=1,out_channels=1,kernel_size=(5,5),padding=2,stride=2)
output = conv2d(a)
output.size()
# 输出为：torch.Size([1, 1, 5, 5])

池化默认也是向下取整

# 池化默认也是向下取整
import torch
import torch.nn as nn
a = torch.rand(1,1,10,10)
# (10+2*2-5)/2.0+1 = 5.5
maxpool = nn.MaxPool2d(kernel_size=(5,5),stride=2,padding=2)
output = maxpool(a)
output.size()
# 输出为：torch.Size([1, 1, 5, 5])

但是，Pytorch中池化层有个参数ceil_node=True是向上取整的，它默认是False，TensorFlow里面没找到类似的参数

# 池化层ceil_mode=True向上取整
import torch
import torch.nn as nn
a = torch.rand(1,1,10,10)
# (10+2*2-5)/2.0+1 = 5.5
maxpool = nn.MaxPool2d(kernel_size=(5,5),stride=2,padding=2,ceil_mode=True)
output = maxpool(a)
output.size()
# 输出为：torch.Size([1, 1, 6, 6])

总结

到这里我们学到了

不同卷积的应用
多维卷积的原理
多维卷积核参数的个数
卷积中的特征图计算方式

是不是感觉收获满满！！！