数据预处理:归一化/标准化详解
前言
一般而言,样本的原始特征中的每一维特征由于来源以及度量单位不同,其特征取值的分布范围往往差异很大,比如身高、体重、血压等它们的度量和分布范围往往是不一样的。当我们计算不同样本之间的欧氏距离时,取值范围大的特征会起到主导作用。这样,对于基于相似度比较的机器学习方法(比如最近邻分类器),必须先对样本进行预处理,将各个维度的特征归一化到同一个取值区间,并且消除不同特征之间的相关性,才能获得比较理想的结果。虽然神经网络可以通过参数的调整来适应不同特征的取值范围,但是会导致训练效率比较低。
归一化的必要性及价值
现在假设一个只有一层的网络:
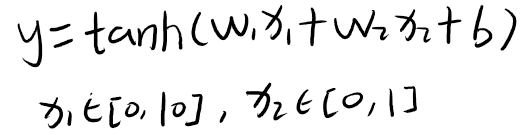
我们知道,tanh 函数的导数在区间 [−2, 2] 上是敏感的,其余的导数接近于 0,tanh图像如下图所示:

因此,如果 过大或过小,都会导致梯度过小,难以训练。为了提高训练效率,我们需要使在 [−2, 2] 区间,我们需要将w1 设得小一点,比如在 [−0.1, 0.1] 之间。可以想象,如果数据维数很多时,我们很难这样精心去选择每一个参数。因此,如果每一个特征的取值范围都在相似的区间,比如 [0, 1] 或者 [−1, 1],那该多好啊,我们就不太需要区别对待每一个参数,减少人工干预。
我们经常见到,归一化、标准化、规范化,其实他们的含义是一样的,都是消除数据量纲带来的差异,加快模型的训练效率
除了参数初始化之外,不同输入特征的取值范围差异比较大时,梯度下降法的效率也会受到影响。下图给出了数据归一化对梯度的影响。其中,图a为未归一化数据的等高线图。取值范围不同会造成在大多数位置上的梯度方向并不是最优的搜索方向。当使用梯度下降法寻求最优解时,会导致需要很多次迭代才能收敛。如果我们把数据归一化为取值范围相同,如图b所示,大部分位置的梯度方向近似于最优搜索方向。这样,在梯度下降求解时,每一步梯度的方向都基本指向最小值,训练效率会大大提高。

归一化的方式
归一化的方法有很多种,最常用的是最小最大归一化和标准归一化
最小最大归一化使结果落到[0,1]区间,转换函数如下:
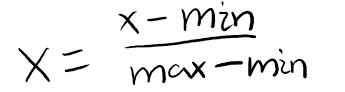
其中 min(x) 和 max(x) 分别是特征 x 在所有样本上的最小值和最大值。
标准归一化也叫 z-score 归一化,将每一个维特征都处理为符合标准正态分布(均值为 0,标准差为 1)。

这里 σ 不能为 0。如果标准差为 0,说明这一维特征没有任务区分性,可以直接删掉。在标准归一化之后,每一维特征都服从标准正态分布。
总结
总的来说,归一化的好处是:帮助你去除数据的量纲和数据大小的差异,让数据每一个特征的取值范围都在相似的区间,可以让数据在同一个数量级下来做一个比较。这样做可以让模型更快的收敛,因为它不需要去考虑那些夸大的特征,把所有特征的尺度看的同等重要
参考文档
神经网络与深度学习[邱锡鹏著]