使用numpy实现逻辑回归对IRIS数据集二分类

发表于2020-07-16更新于2022-06-05字数统计1.3k阅读时长12分

使用numpy实现逻辑回归对IRIS数据集二分类，使用对数似然损失(Log-likelihood Loss)，并显示训练后loss变化曲线。

知识储备如下：

  • 逻辑回归Logistic Regression
  • 对数似然损失
  • IRIS数据集介绍
  • np.concatenate使用

知识储备

逻辑回归Logistic Regression

y=11+e−(wx+b)y = \frac{1}{1+e^{-(wx+b)}}

名字虽然叫回归，但是一般处理的是分类问题，尤其是二分类，比如垃圾邮件的识别，推荐系统，医疗判断等，因为其逻辑与实现简单，在工业界有着广泛的应用。

优点：

  • 实现简单，计算代价不高，易于理解和实现, 广泛的应用于工业问题上；
  • 分类时计算量非常小，速度很快，存储资源低；

缺点：

  • 容易欠拟合，当特征空间很大时，逻辑回归的性能不是很好；
  • 不能很好地处理大量多类特征或变量；

对数似然损失

对数损失, 即对数似然损失(Log-likelihood Loss), 也称逻辑斯特回归损失(Logistic Loss)或交叉熵损失(cross-entropy Loss), 是在概率估计上定义的。它常用于(multi-nominal, 多项)逻辑斯特回归和神经网络,以及一些期望极大算法的变体,可用于评估分类器的概率输出。可参考对数损失函数(Logarithmic Loss Function)的原理和 Python 实现了解详情

损失函数:

L=1m∗∑im−yilog(f(xi))−(1−yi)log(1−f(xi))L=\frac{1}{m}*\sum_i^m -y_ilog(f(x_i))-(1-y_i)log(1-f(x_i))

梯度计算：

∂L∂w=1mXT∗(f(x)−y)\frac{\partial L}{\partial w} = \frac{1}{m}X^T*(f(x)-y)

权重更新：

w=w−α∂L∂ww = w -\alpha\frac{\partial L}{\partial w}

IRIS数据集介绍

该数据集包含4个特征变量，1个类别变量。iris每个样本都包含了4个特征：花萼长度，花萼宽度，花瓣长度，花瓣宽度，以及1个类别变量（label）。详情见加载数据

np.concatenate使用

1
2
3
a = np.array([[1, 2],[3, 4]])
b = np.array([[5, 6]])
np.concatenate((a, b), axis = 0)
array([[1, 2],
       [3, 4],
       [5, 6]])

1
np.concatenate((a, b.T), axis = 1)
array([[1, 2, 5],
       [3, 4, 6]])

加载数据

1
2
3
4
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
%matplotlib inline
1
2
3
4
5
6
7
dataset = load_iris()
inputs = dataset['data']
target = dataset['target']
print('inputs.shape:', inputs.shape)
print('target.shape:', target.shape)
# 三个类别
print('labels:', set(target))
inputs.shape: (150, 4)
target.shape: (150,)
labels: {0, 1, 2}

1
target
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

1
2
3
values = [np.sum(target == 0), np.sum(target == 1), np.sum(target == 2)]
plt.pie(values,labels=[0, 1, 2], autopct = '%.1f%%')
plt.show()

关于参数train_test_split的random_state的解释：

Controls the shuffling applied to the data before applying the split. Pass an int for reproducible output across multiple function calls.
random_state即随机数种子，目的是为了保证程序每次运行都分割一样的训练集和测试集。否则，同样的算法模型在不同的训练集和测试集上的效果不一样。

1
2
3
4
5
6
7
8
9
10
11
from sklearn.model_selection import train_test_split
# 只取前两类， 做二分类
two_class_input = inputs[:100]
two_class_target = target[:100]
x_train, x_test, y_train, y_test = train_test_split(
                    two_class_input,two_class_target,
                    test_size = 0.3,
                    random_state = 0)
y_train = y_train.reshape(-1,1)
y_test = y_test.reshape(-1,1)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
(70, 4) (30, 4) (70, 1) (30, 1)

1
2
3
4
# add one feature to x
x_train = np.concatenate([x_train, np.ones((x_train.shape[0], 1))], axis = 1)
x_test = np.concatenate([x_test, np.ones((x_test.shape[0], 1))], axis = 1)
print(x_train.shape, x_test.shape)
(70, 5) (30, 5)

定义模型

1
2
3
4
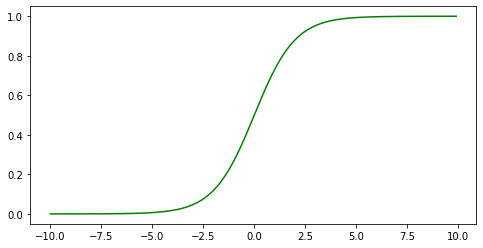
5
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
x = np.arange(-10, 10, step = 0.1)
fig, ax = plt.subplots(figsize = (8, 4))
ax.plot(x, sigmoid(x), c = 'green')
[<matplotlib.lines.Line2D at 0x28f77053348>]


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
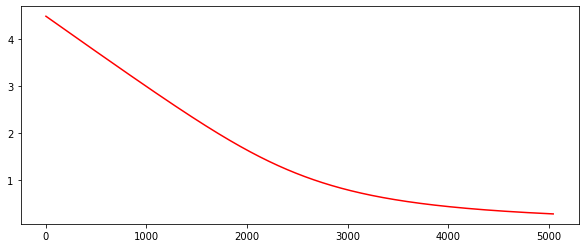
24
compute_loss = lambda pred_y, y: np.mean(-y * np.log(pred_y)-(1-y) * np.log(1-pred_y))
# weight and bias init
w = np.random.randn(5, 1)
# 上一个loss
losses = []
last_loss = 10000
pred_y =sigmoid(np.dot(x_train, w))
# 当前loss
now_loss = compute_loss(pred_y, y_train)
i = 0
while abs(now_loss - last_loss)>1e-4:
    last_loss = now_loss
    i = i + 1
    # 计算梯度
    grad = x_train.T.dot((pred_y - y_train)) / len(y_train)
    # 更新梯度
    w = w - 0.001 * grad
    
    # 前导计算
    pred_y = sigmoid(np.dot(x_train, w))
    now_loss = compute_loss(pred_y, y_train)
    losses.append(now_loss)
fig, ax = plt.subplots(figsize = (10, 4))
ax.plot(np.arange(len(losses)), losses, c = 'r')
[<matplotlib.lines.Line2D at 0x28f77053508>]

测试样例

1
2
3
4
5
# 测试
test_pred = sigmoid(np.dot(x_test, w))
pre_test_y = np.array(test_pred > 0.5, dtype = np.float32)
acc = np.sum(pre_test_y == y_test) / len(y_test)
print("the accary of model is {}".format(acc*100))
the accary of model is 100.0

1
2
print(pre_test_y.reshape(1,-1))
print(y_test.reshape(1,-1))

[[0. 1. 0. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 1. 0. 0. 0. 1. 1. 1.]]
[[0 1 0 1 1 1 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 1 1]]