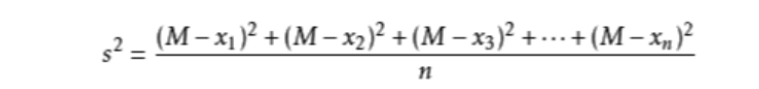使用numpy实现线性模型预测boston房价

发表于2020-07-16更新于2022-06-05字数统计1.5k阅读时长12分

使用numpy实现线性模型预测boston房价，激活函数为Relu，使用MSE_loss，手动求导，并显示训练后loss变化曲线。

知识储备如下：

  • Scikit-learn
  • boston房价数据解读
  • 标准差公式
  • Linear及MSE_loss求导公式

知识储备

Scikit-learn

Scikit-learn(sklearn)是机器学习中常用的第三方模块，对常用的机器学习方法进行了封装，包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类(Clustering)等方法。其优点为：

  • 简单高效的数据挖掘和数据分析工具
  • 让每个人能够在复杂环境中重复使用
  • 建立NumPy、Scipy、MatPlotLib之上

安装方法 pip install scikit-learn

boston房价数据解读

使用sklearn.datasets.load_boston即可加载相关数据。该数据集是一个回归问题。每个类的观察值数量是均等的，共有506个观察，13个输入变量和1个输出变量。每条数据包含房屋以及房屋周围的详细信息。其中包含城镇犯罪率，一氧化氮浓度，住宅平均房间数，到中心区域的加权距离以及自住房平均房价等等，具体如下：

  • CRIM：城镇人均犯罪率。
  • ZN：住宅用地超过 25000 sq.ft. 的比例。
  • INDUS：城镇非零售商用土地的比例。
  • CHAS：查理斯河空变量（如果边界是河流，则为1；否则为0）。
  • NOX：一氧化氮浓度。
  • RM：住宅平均房间数。
  • AGE：1940 年之前建成的自用房屋比例。
  • DIS：到波士顿五个中心区域的加权距离。
  • RAD：辐射性公路的接近指数。
  • TAX：每 10000 美元的全值财产税率。
  • PTRATIO：城镇师生比例。
  • B：1000（Bk-0.63）^ 2，其中 Bk 指代城镇中黑人的比例。
  • LSTAT：人口中地位低下者的比例。
  • MEDV：自住房的平均房价，以千美元计。
  • 预测平均值的基准性能的均方根误差（RMSE）是约 9.21 千美元。

标准差公式

如x1,x2,x3…xn的平均数为M，则方差可表示为：

样本标准差=方差的算术平方根=s=sqrt(((x1-x)^2 +(x2-x)^2 +…(xn-x)^2)/(n-1) )
总体标准差=σ=sqrt(((x1-x)^2 +(x2-x)^2 +…(xn-x)^2)/n )
如是总体，标准差公式根号内除以n
如是样本，标准差公式根号内除以（n-1)。
因为我们大量接触的是样本，所以普遍使用根号内除以（n-1)。

1
2
a=np.array([[1,2,3],[4,5,6]])
np.mean(a,axis=1)
array([2., 5.])

1
2
# axis = 1表示行，ddof = 1是除以n-1
np.std(a, axis = 1,ddof = 1)
array([1., 1.])

1
2
# ddof默认为0,是除以n
np.std(a, axis = 1)
array([0.81649658, 0.81649658])

1
2
# 求所有数平均值
np.mean(a)
3.5

Linear及MSE_loss求导公式

损失函数
L=12N∑i=1N(zi−yi)2L = \frac{1}{2N}\sum_{i=1}^{N}(z^{i} - y^{i})^{2}

线性函数
zi=∑j=0Nxj(i)w(j)+b(j)z^i = \sum_{j=0}^{N}x_j^{(i)}w^{(j)} + b^{(j)}

对 ww 偏导，得到ww 更新梯度
∂L∂wj=1N∑iN(z(i)−y(i))xj(i)\frac{\partial L}{\partial w_j} = \frac{1}{N}\sum_{i}^{N}(z^{(i)} - y^{(i)})x_j^{(i)}

对 bb 偏导，得到bb 更新梯度
∂L∂b=1N∑iN(z(i)−y(i))\frac{\partial L}{\partial b} = \frac{1}{N}\sum_{i}^{N}(z^{(i)} - y^{(i)})

数据加载

1
2
3
from sklearn.datasets import load_boston
import numpy as np
import matplotlib.pyplot as plt
1
2
3
4
5
6
7
data = load_boston()
X_ = data['data']
y = data['target']
print(type(data), type(X_), type(y))
print('data keys:', data.keys())
print('X_.shape:', X_.shape)
print('y.shape:', y.shape)

<class 'sklearn.utils.Bunch'> <class 'numpy.ndarray'> <class 'numpy.ndarray'>
data keys: dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename'])
X_.shape: (506, 13)
y.shape: (506,)

数据规范化

1
2
3
4
5
# 转化为标准正态分布
X_ = (X_ - np.mean(X_, axis=0)) / np.std(X_, axis = 0)
y = y.reshape(-1,1) # reshape转化为vector
print(X_.shape)
print(y.shape)

(506, 13)
(506, 1)

建立激活函数

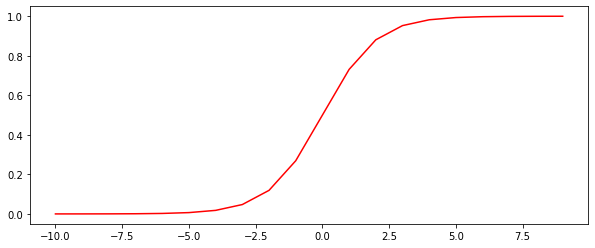
1
2
3
4
5
6
def sigmoid(x):
    r = 1 / (1 + np.exp(-x))
    return r
nums = np.arange(-10, 10, step = 1)
fig, ax = plt.subplots(figsize = (10, 4))
ax.plot(nums, sigmoid(nums), c='red')

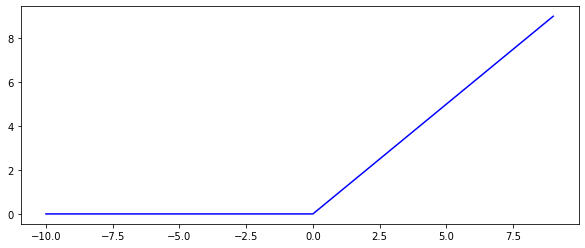
1
2
3
4
5
def relu(x):
    return (x > 0) * x
fig, ax = plt.subplots(figsize = (10, 4))
nums = np.arange(-10, 10, step = 1)
ax.plot(nums, relu(nums), c = 'blue')

定义模型

线性模型：y=wx+by = wx + b

1
2
3
def Linear(x, w, b):
    y_pre = x.dot(w) + b
    return y_pre

在计算损失时，需要把每个样本的损失都考虑到，所以我们需要对单个样本的损失函数进行求和，并除以样本总数N。

1
2
3
def MSE_loss(y_pre, y):
    loss = np.mean(np.square(y_pre - y))
    return loss
1
2
3
4
5
def gradient(x, y_pre, y):
    n = x.shape[0]
    grad_w = x.T.dot(y_pre - y)/n
    grad_b = np.mean(y_pre - y)
    return grad_w, grad_b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 初始化网络
n = X_.shape[0] # 样本数量506
n_features = X_.shape[1] #特征数量13

# 初始化网络参数
# randn从标准正态分布中返回一个或多个样本值
W = np.random.randn(n_features, 1)
b = np.zeros(1)

#设定学习率
learning_rate = 1e-2

#训练次数
epoch = 10000

训练(不加激活函数)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
losses = []
# 训练 
for t in range(epoch):
    # 向前传播
    y_pred = Linear(X_, W, b)
    # 计算损失函数
    loss = MSE_loss(y_pred,y)
    losses.append(loss)
    grad_w, grad_b = gradient(X_, y_pred, y)
    
    #权重更新
    W = W - grad_w * learning_rate
    b = b - grad_b * learning_rate

fig, ax = plt.subplots(figsize = (10, 4))
ax.plot(np.arange(len(losses)), losses, c = 'r')

1
2
3
4
5
n_hidden = 10 #设计隐藏神经元个数（可修改）
W1 = np.random.randn(n_features, n_hidden)  # 维度 n_features * n_hidden
b1 = np.zeros(n_hidden)                     # 维度 1 * n_hidden
W2 = np.random.randn(n_hidden, 1)           # 维度 n_hidden * 1
b2 = np.zeros(1)                            # 维度1

训练(加激活函数)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 训练
losses = []
for t in range(epoch):
    #向前传播
    y_pred1 = Linear(X_, W1, b1)     # 维度 n * n_hidden
    y_relu = relu(y_pred1)           # 维度 n * n_hidden
    y_pred = Linear(y_relu, W2, b2) # 维度 n * 1
    
    #计算损失函数
    loss = MSE_loss(y_pred, y)
    losses.append(loss)
    
    #反向传播，求梯度
    grad_y_pred = y_pred - y                 # 维度n*1
    grad_w2 = y_relu.T.dot(grad_y_pred) / n  # 维度n_hidden*1
    grad_b2 = np.mean(grad_y_pred, axis = 0) # 维度1*1
    grad_relu = grad_y_pred.dot(W2.T)        # 维度n*n_hidden
    #注意：y_pred1与relu直接相关
    grad_relu[y_pred1 < 0] = 0
    grad_w1 = X_.T.dot(grad_relu) / n        # 维度n_features* n_hidden
    grad_b1 = np.mean(grad_relu, axis = 0)   # 维度n_hidden*1
    
    #更新梯度
    W1 = W1 - grad_w1 * learning_rate
    b1 = b1 - grad_b1 * learning_rate
    W2 = W2 - grad_w2 * learning_rate
    b2 = b2 - grad_b2 * learning_rate

fig, ax = plt.subplots(figsize = (10, 4))
ax.plot(np.arange(len(losses)), losses, c = 'r')

参考文档

波士顿房价数据集解读